Miguel A. Martín Delgado on the cover of PHYSICAL REVIEW LETTERS!

Optimal Thresholds for Fracton Codes and Random Spin Models with Subsystem Symmetry.

Phys. Rev. Lett. 129, 230502 – Published 30 November 2022

Issue: Vol. 129, Iss. 23 — 2 December 2022

Abstract:
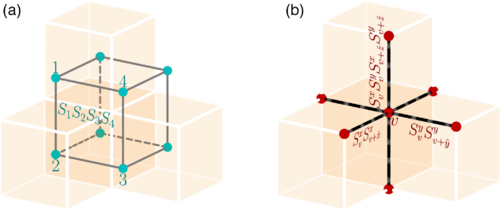
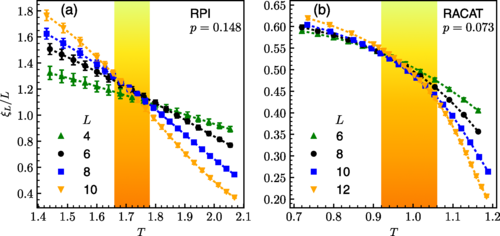
Fracton models provide examples of novel gapped quantum phases of matter that host intrinsically immobile excitations and therefore lie beyond the conventional notion of topological order. Here, we calculate optimal error thresholds for quantum error correcting codes based on fracton models. By mapping the error-correction process for bit-flip and phase-flip noises into novel statistical models with Ising variables and random multibody couplings, we obtain models that exhibit an unconventional subsystem symmetry instead of a more usual global symmetry. We perform large-scale parallel tempering Monte Carlo simulations to obtain disorder-temperature phase diagrams, which are then used to predict optimal error thresholds for the corresponding fracton code. Remarkably, we found that the X-cube fracton code displays a minimum error threshold (7.5%) that is much higher than 3D topological codes such as the toric code (3.3%), or the color code (1.9%). This result, together with the predicted absence of glass order at the Nishimori line, shows great potential for fracton phases to be used as quantum memory platforms.

• 

• 

• 

• 

DOI: https://doi.org/10.1103/PhysRevLett.129.230502

Published by the American Physical Society under the terms of the Creative Commons Attribution 4.0 International license. Further distribution of this work must maintain attribution to the author(s) and the published article’s title, journal citation, and DOI.